Vertical Turbine Pump – Vibration and Stress Analysis for Submerged Structures per ASCE 4-98

Vertical Turbine Pump – Vibration and Stress Analysis for submerged structures per ASCE 4-98 FEA Vibration Engineering Structures Immersed in Water

Analysis

FEA

Objective

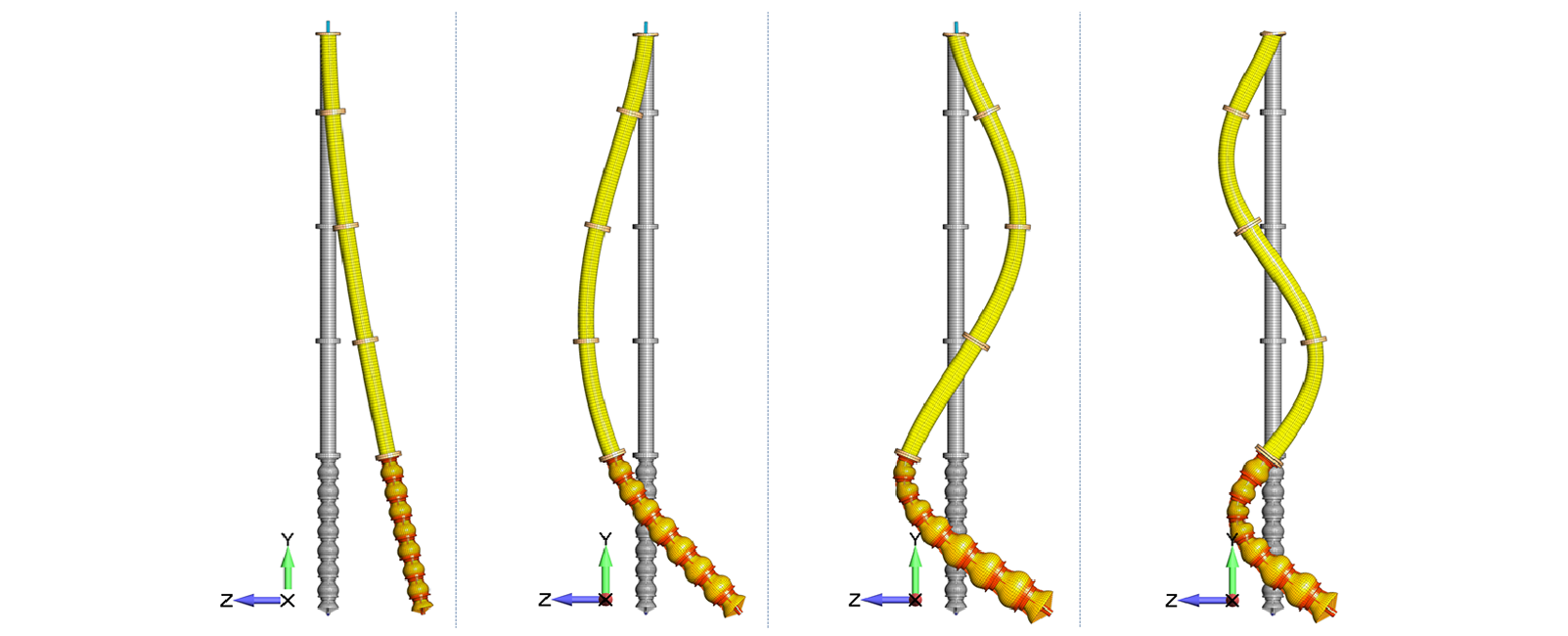
The vibration requirements of this project state that “The complete pumping unit…shall be free from dangerous critical speeds from 20 percent below to 30 percent above the operating speeds required to achieve the specified performance characteristics.” In simpler terms, this means it was imperative to identify the normal modes of the structure and ensure that they would not be excited by operation of the equipment (see Figure 1).

In general, this is an easy and straightforward FEA analysis. In the case of this project, a bit more preparation was required before running through the standard steps of the FEA procedure. Submerging a structure into fluid will have a dramatic effect on the damping and natural frequency of the structure. With the guidance of Wambsganss, et al., “Added Mass and Damping of a Vibrating Rod in Confined Viscous Fluids” the mass of the structure was adjusted to account for the effects of the fluid surrounding the pump within the confines of the pump can.  This reference also refers to the ground breaking work by R.J. Fritz “The Effect of Liquids on the Dynamic Motions of Immersed Solids”, Journal of Engineering for Industry, 1972. According to this discussion, the effects of surrounding fluid can be modeled as added-mass terms in the component structure mass matrix. Aside from some support plates, the internal components in the vessels are all cylindrical objects.

PDF Download

vibration_and_stress_analysis_of_vertical_turbine_pump_per_asce_4-98.pdf (541.9 KB)
Normal mode shapes of the vertical pump with added mass (Fritz) - Vibration of Submerged Pumps, Vessels and Structures
Normal mode shapes of the vertical pump with added mass (Fritz) - Vibration of Submerged Pumps, Vessels and Structures - FEA Consulting Services
FE modeling and idealization techniques using plate elements for beam elements, mass elements and rigid body elements - Digital Prototyping of Pump Systems into Efficient Vibration Simulations
The above images show in detail, the FE modeling and idealization techniques using plate elements, beam elements, mass elements and rigid body elements.
FE modeling and idealization techniques using plate elements for beam elements, mass elements and rigid body elements - Digital Prototyping of Pump Systems into Efficient Vibration Simulations - Predictive Engineering